 Turm von Hanoi mit 7 runden Scheiben Logikspiel in einer Holzbox in Maßen 21,0 x 8,4 x 3,5 cm , pagoda 7 level samanea wooden puzzle
Turm von Hanoi mit 7 runden Scheiben Logikspiel in einer Holzbox in Maßen 21,0 x 8,4 x 3,5 cm , pagoda 7 level samanea wooden puzzle
Turm von Hanoi 7 Rund
Turm von Hanoi

Der Turm von Hanoi kann aus drei bis sieben Scheiben bestehen. Der gesamte Turm soll, mit den verschiedenen Scheibengrössen, vom Mittelpfosten zum rechten oder linken Pfosten umgestapelt werden. Der jeweilige dritte Pfosten rechts oder links ist der Hilfsplatz (Ausweichplatz),notwendig um die nicht benötigte Scheibe zu parken, damit die Scheiben der richtigen Reihenfolge aufgestapelt werden können. Es kann nur die oberste Scheibe vom einem Turm bewegt werden. Es kann nie eine grössere Scheibe auf eine kleinere Scheibe gelegt werden, sondern immer kleine Scheiben auf große Scheiben.
Hier eine leichte Varriante zum üben mit 3 Scheiben: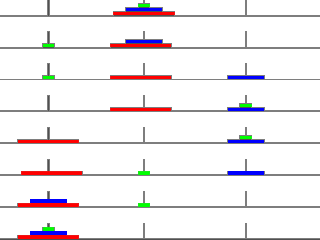
Wir beginnen in der Mitte mit 3 Scheiben. nehmen die kleinste grüne Scheibe nach links. Danach nehmen wir die mittlere blaue Scheibe nach rechts. Hierrauf setzen wir die kleinste grüne Scheibe von links nach ganz rechts. Um dann die rote größte Scheibe nach links zu setzen. Nun setzen wir die grüne in der Mitte ab um die blaue Scheibe auf die rote zu setzen. Zumm Schluß die grüne oben drauf und der turm steht links. Das ist der schnellste und kürzeste Weg den Turm nach den Regeln umzustapeln. Zurück probiers allein. Viel Spass.
Solltest Du trotzdem nich weiter kommen oder möchtest 4 oder 7 Ringe probieren schaust Du hier nach mehr Hilfe: Turm von Hanoi Lösung











